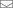Построение годографа точки звуковой волны в изотропной среде при изменении ветра по высоте в вертикальной плоскости

Деформация звуковой волны при линейном увеличении скорости ветра с ростом высоты в интервале времени от 1до 15 сек. Шаг времени 1 сек.
В.А. Крюков
VAK_53@mail.ru
В первой статье https://habr.com/ru/articles/795963/ была рассмотрена конечная формула звуковой волны, распространяющейся в равновесной неподвижной среде от источника звука на земле. Перейдем более интересной задаче Рэлея, когда скорость ветра возрастает с высотой по линейному закону. Известно, что Рэлей получил для этого случая уравнение звукового луча в вертикальной плоскости в виде цепной линии.
В предыдущей статье было обещано, что будет рассказано о программе–демонстраторе численного интегрирования годографа точки звуковой волны. В программе–демонстратор учитывается деформацию полусферической звуковой волны, которое вызывает искривление звуковых лучей от ветра, характеризующегося увеличением скорости с ростом высоты.
1. История вопроса
Рис. 1, взятый из учебника по артиллерийской разведке [1], качественно показывает ход звуковых лучей в рассматриваемом здесь случае увеличения скорости ветра с ростом высоты.

Рис. 1 Наблюдаемое искривление звуковых лучей при градиентном ветре.
На Рис. 1 слева с наветренной стороны показана зона акустической тени. Справа с подветренной стороны часть низких лучей «заземляются».
Объяснений этому факту первым дал Стокс, который указал на необходимость принимать во внимание возрастание скорости ветра с высотой. В таких условиях луч, распространяющийся по ветру, будет изгибаться вниз, а луч, распространяющийся против ветра, будет изгибаться вверх.
Как я уже писал в предыдущей статье Лорд Релей получил для линейного изменения скорости ветра в вертикальной плоскости формулу преломления звукового луча в виде цепной линии. Метод Гамильтона в акустике движущихся сред при возрастании скорости ветра с высотой по линейному закону и всюду постоянной скорости звука приводит к уравнению луча в виде окружности вместо цепной линии [2].
Что касается изменения скорости ветра по высоте, этот вопрос нуждается в отдельном комментировании. Модель линейного увеличений скорости с ростом высоты — не более, чем дань более чем 100 летней традиции постановки вопроса. При ламинарном потоке скорость ветра в пограничном слое растет по полиномиальному закону [3]. С какой–то высоты ветер не меняет своей скорости. Поэтому, по–хорошему, приземному ветру нужно задавать профиль, накладывая следующие условия:
v = 0 при z =0
v = v∞ и $\frac{dv}{dz}=0$ при z = δ
, где δ — толщина пограничного слоя.
Этот вопрос нуждается в отдельном рассмотрении.
2. Постановка задачи.
Первичная задача — понять, какую форму принимает полусфера в условиях линейного увеличения скорости ветра с ростом высоты. Таким образом, можно будет смоделировать искажения хода звуковых лучей в вертикальной плоскости. Это классическая постановка задачи по Релею.
В левой части Рис. 2 показана окружность сферы звуковой волны в вертикальной плоскости xz. Звуковая волна распространяется в форме полусферы, но для дальнейшего удобства лучше рассматривать сферу. Источник звука находится в центре сферы/окружности.
Скорость ветра с высотой растет по линейному закону:
v=v0+kz
Будем рассматривать приземный поток воздуха как пограничный слой. Тогда на уровне земли примем скорость ветра нулевой v0=0 и формула упростится.
Размерностью k будет [1/c]
Вид деформированной полусферической звуковой волны в вертикальной плоскости будет описываться формулами:
$z_{волн}= z_{окр}$ | (2) |
$x_{волн}= x_{окр}+vt_T=x_{окр}+kzt_T$ |
, где xокр и zокр являются координатами виртуальной окружности полусферической звуковой волны,
v — скорость ветра в точке профиля волны по формуле (1),
tT — время прохождения волны до данного профиля; удобно универсально привязать время к верхней точке профиля.
Таким образом, разрез фронта звуковой волны представляет собой не полуокружность полусферы, а фигура, которая получается в результате деформации сдвига, задаваемый линейным преобразованием (2). См. Рис. 2.

Рис. 2 Деформация звуковой волны.
Для удобства рассмотрения дальнейших преобразований эллипса он нарисован полностью.
Из рисунка видно, что писанный вокруг окружности квадрат преобразуется в ограничивающий параллелограмм, а круг превращается в эллипс, вписанный в этот параллелограмм. Высота верхней точки профиля звуковой волны T«смещается на ctT, где
c — скорость звука,
tT— время распространения волны.
Угол наклона стороны параллелограмма определяется линейным приращением координаты x по формуле (2). Эллипса сохраняет касание к параллелограмму, в том числе в верхней точке T».
Горизонтальным диаметр эллипса не претерпевает изменения размера. Сопряженный ему диаметр T«B» отклоняется от вертикали.
Определим наклон сопряженного диаметра T«B», а затем направление большой оси эллипса. Точка T» отклоняется от вертикальной оси z на величину vtT. Высота точки T» по сравнению точкой T на левой окружности не изменяется. Тогда согласно (1):
$$tg\alfa= \frac{TT^'}{OT} = \frac{v_Tt_T}{ctT}=\frac{v_T}{c} = \frac{kz_T}{c}$$
Отношение величин vT=kzT << c. С ростом zT tgα и угол α будут соответственно расти, и ограничивающий параллелограмм будет сильнее отклоняться по ветру.
Не будем учитывать перепады температуры по высоте и примем за среднюю скорость звука в диапазоне от 0 до ~1000 м величину 333,3 м/с. См. реплику о пограничном слое в разделе «История вопроса».
Положим, что на максимальной высоте v=18 м/с. Тогда угол наклона сопряженного диаметра будет:
$\alfa_{1000}=atan\frac{\frac{18}{1000}1000}{333,3}\approx3° $
Можно сказать, что 3° это немного.
На расстоянии 5 км угол α уже существенно возрастает:
$\alfa_{5000}=atan\frac{\frac{18}{1000}5000}{333,3}\approx15.11° $
Для наглядности приведем рисунок данного профиля звуковой волны. См. Рис. 3. Построен эллипс по 5–ти известным точкам:
· Верхняя точка профиля T»,
· Нижняя виртуальная точка B»
· Правая зафиксированная точка R,
· Левая зафиксированная точка L.
В качестве пятой точки можно принять произвольную расчетную точку профиля. В данном случае это точка A с левой стороны.

Рис. 3 Профиль деформированной звуковой волны на высоте 5000 м при скорости ветра 90 м/с.
Конечно, бессмысленно строить профиль волны на высоте 5 км. т.к. наша цель — исследовать прохождение звуковых лучей в приземном слое. Поэтому считайте такой профиль виртуальным. На практике в 3–D измерении будет использоваться горизонтальный пояс эллипсоида, но все по порядку.
Вернемся к нашему наклонному эллипсу. Наклон большой оси эллипса совпадает по направлению с большой диагональю ограничивающего параллелограмма. Для эллипса на графике он равен 37,44º. Даже при ctT=1000 м он будет тоже значительным:
$\beta=\frac{90–3}{2}= 43,5º$
Можно предположить, что именно большая величина наклона большой оси эллипса вправо и даёт то искривление звуковых лучей, качественно показанное на Рис. 1.
3. Описание алгоритма программы–демонстратора.
Программа–демонстратор написана на Python. Алгоритм программы достаточно простой, но есть нюансы.
Входные данные:
· Начальное и конечное время звуковой волны. Шаг интегрирования годографов.
· Скорость ветра и высота, на которой ветер достигает заданного значения.
· Несколько углов инициализации лучейφ1.
Алгоритм:
1) Определение начального профиля звуковой волны.
Начальным профилем вполне можно привязать к отметке времени 1 сек. При такой отметки времени профиль будет иметь очень маленьким угол наклона ограничивающего параллелограмма:
$\alfa_{1}=atan\frac{\frac{18}{1000}1}{333,3}\approx0,003° $
т.е. можно считать эллиптический профиль недеформированной окружностью, у которого лучи ещё прямолинейные.
1) Определение на профиле по заданным начальным углам инициализации координаты исходных точек лучей. Координаты начальных точек лучей добавляются в соответствующие списки.
2) Вход в цикл генерации следующих эллипсов деформированной звуковой волны с шагом Δt.
a) Генерация эллипса деформированной звуковой волны для данной отметки времени.
b) Приведение сгенерированного эллипса в общем виде к каноническому виду.
c) Разворачивание вслед за эллипсом концевых точек лучей по часовой стрелке на угол -β сгенерированного эллипса
d) Опускание нормалей из концевых точек лучей на сгенерированный эллипс.
e) Разворот точек оснований нормалей против часовой на угол β и дополнение ими списков координат точек лучей.
f) Проверка условия достижения конечного времени распространения луча. При выполнении условия выход из цикла.
g) Переход на начало цикла.
3) При необходимости анализ списков координат точек лучей. Рисование графиков годографов по спискам координат.
Важным центральным компонентом программы является подпрограмма опускания нормали из конечной точки луча на эллипс. Алгоритм подпрограммы был позаимствован на сайте [4].
4. График годографов моделирования хода звуковых лучей.
Входными данными являются:
· На высоте 1000 м ветерсильный w=18 м/c.
· Время распространения волны от 1с до 31c
· Начальный уголφ1 от 10° до 180° через каждые 10°.
Скорость приземного ветра нулевая. Результаты моделирования показаны на Рис. 4

Рис. 4. Годографы с начальными углами от 10° до 180° через 10°.
Как показал лорд Релей ещё лет 150 назад, прямые лучи звуковой волны искривляются. Но теперь мы знаем причину искривления лучей из–за деформации формы звуковой волны в эллипсоид. С наветренной стороны мы наблюдаем зоны тишины. С правой стороны лучи «заземляются» в землю.
Дальше результаты неожиданные. При ~40 и ~130 градусов лучи почти прямые! Прямые! Как это можно объяснить? Если посмотреть на чертеж эллипсов звуковых волн (например, см. Рис. 3), то можно понять, что эти направления близки или совпали с большой и малой осью эллипсов. Таким образом, лучи «катят» свободно по осевым линиям эллипса.
А в секторе между ~40 и ~130 градусами лучи изгибаются влево?! По учебникам должны изгибаться вправо. Можно, конечно, сослаться на неточность модели линейного изменения ветра по высоте. Это так. Но если поглядеть на картинку с чередой звуковых волн, изображенных на кате, то можно заметить, что в указанном секторе рисунок профилей звуковых волн очень похож на рисунок профилей при постоянном ветре (первая статья), и лучи именно так и должны искривляться влево. Эффект неожиданный и до сих пор не предсказанный.
На показанной диаграмме обращает на себя внимание тот факт, что с подветренной стороны после 10 км. очень неплотная звуковая волна с рассеянной энергией.
Более детальные данные показывают, что на расстояния -125 м горизонтальный луч 180º поднимается на высоту 4 м. Там начинается гарантированная зона тишины.
5. Прагматическая сторона вопроса
Время работы программы–демонстратора расчета 5 годографов на расстояние 10 км составляет 74 мс. Время обратной трассировки годографов от наблюдателя к точке источника звука будет меньше, т.к. итерационный алгоритм поиска нормали на эллипс заменяется на прямой алгоритм восстановления нормали.
6. Проверки методики
Проверку метода численного интегрирования вдоль годографа точки ударной волны можно провести, сравнивая результаты представленного метода при постоянной скорости ветра с результатами ранее рассмотренного метода аналитического задания годографа, согласно первой статьи.
Входные данные проверки:
· Ветерсильный w=18 м/c, чтобы визуально наблюдать кривизну.
· Начальный угол φ1 = ±15°; ±60°; ±115; ±170°.
· Время распространения волны до t = 21c. Интервал времени 1с.
Результаты проверки показаны на Рис. 5

Рис. 5. Наложенные годографы с начальными углами 15°, 60°, 115° и 170°, рассчитанные двумя методами при постоянной скорости ветра.
Как видно из рисунка, совпадение результатов почти полное. Небольшое расхождение связано с великоватым шагом численного интегрирования, равным 1 сек.
Заключение
Установлено, что при линейном изменении скорости ветра по высоте сечение звуковой волны вертикальной плоскостью преобразуется в наклоненный эллипс. В трехмерном пространстве звуковая волна принимает форму эллипсоида. На базе геометрической акустики получена программа–демонстратор распространения энергия звуковой волны в изотропной среде, движущейся с градиентом скорости (в вертикальной плоскости).
В предыдущей статье была получена конечная формула закона распространения энергия звуковой волны в изотропной равномерно движущейся среде (в горизонтальной плоскости).
Чтобы обобщить найденные решения на трехмерный случай достаточно будет воспользоваться принципом суперпозиции отдельных движений в горизонтальной и вертикальной плоскостях.
Представляет практический интерес программа обратной трассировки звуковых лучей. Но пока я делать этого не буду. В принципе, с алгоритмом там почти всё ясно, и пытливый читатель сможет сделать это самостоятельно, а считаю важным разобраться с профилированием скорости ветра в пограничном слое.
Чтобы читатели не потеряли интерес к поднятой теме, постараюсь в ближайшее время выдать статьи об устройстве приёмника со звуковым датчиком в технологии обработки данных в потоке. Есть нюансы.
Литература
1. Артиллерийская звуковая разведка, изд. МО, М., 1993
2. Чернов Л.А. «Акустика движущейся среды. Обзор», Акустический журнал, 1958, 4, выпуск 4, с. 299–306
3. Абрамович, Прикладная газовая динамика, ГИТТЛ, М., 1953.
4. https://mpewsey.github.io/2021/11/07/minimum-distance-between-ellipse-and-point.html