Оптимальное управление обратным маятником, пример реализации модели в MATLAB01.03.2024 15:45

Классическим примером демонстрации возможностей теории управления является модель обратного маятника на тележке. В данной статье продемонстрируем решение классических проблем классическими методами, но в максимально тепличных условиях, когда всю рутинную работу за нас будут выполнять алгоритмы пакета MATLAB.

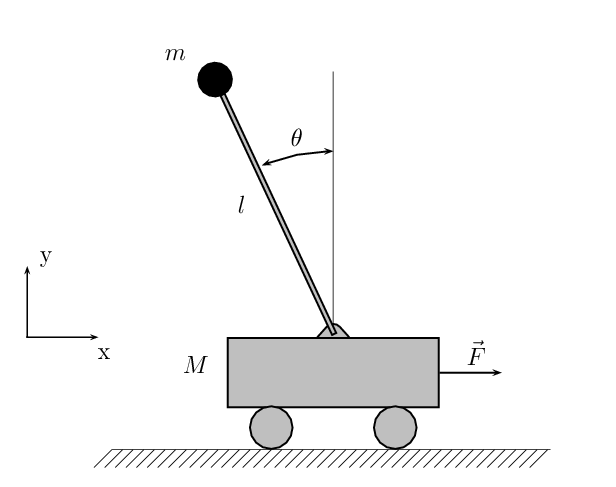
Задачей будет стабилизировать систему, представляющую собой маятник, в положении «вверх», который находится на тележке, которая контролируется внешней силой . В нашем распоряжении есть датчики измерения угла $\theta$ и координаты положения тележки . Нам надо рассчитать такой контроллер, который обеспечит стабильное положение маятника «вверх» при движении тележки и при шумах датчиков.

1. Составление уравнений системы (Plant)

Первым делом необходимо составить модель системы, для чего воспользуемся формулами Лагранжевой механики.

Запишем энергии и скорости системы, где: — масса тележки (kg), — масса маятника (kg), — коэффициент трения (s^-1), — длинна маятника (m), — ускорение силы тяжести (m/s^2).

syms t d M m h v_C v_P x(t) theta(t) l g
TC = 1/2*M*v_C^2; % кинетическая энергия тележки
TP = 1/2*m*v_P^2; % кинетическая энергия маятника
U = m*g*h; % потенциальная энергия
U = subs(U,h,l*cos(theta)); % подставим координату y маятника
v_C = diff(x,t); % скорость тележки
v_P = sqrt(diff(x-l*sin(theta),t)^2 + diff(l*cos(theta),t)^2); % скорость маятника

$T_C =\frac{M\,{v_C }^2 }{2}, T_P =\frac{m\,{v_P }^2 }{2}, U_p =g\,l\,m\,\cos \left(\theta \left(t\right)\right), V_C =\frac{\partial }{\partial t}\;x\left(t\right), V_P =\sqrt{{{\left(\frac{\partial }{\partial t}\;x\left(t\right)-l\,\cos \left(\theta \left(t\right)\right)\,\frac{\partial }{\partial t}\;\theta \left(t\right)\right)}}^2 +l^2 \,{\sin \left(\theta \left(t\right)\right)}^2 \,{{\left(\frac{\partial }{\partial t}\;\theta \left(t\right)\right)}}^2 }$

Из закона сохранения энергии найдем выражение для Лагранжиана $L\left(t,q,q^{\prime } \right)$ , где: $q=\left(x\left(t\right),\theta, q^{\prime } =\left(V_C \left(t\right),V_P \left(t\right)\right) \left(t\right)\right)$

syms F_ext % внешняя сила
L = subs(exp(d*t)*(TC + TP - U + x*F_ext)); % exp(d*t) - множитель для учета трения

Найдем уравнения системы с помощью выражения Лагранжевой механики $\frac{\mathrm{d}}{\mathrm{d}t}\frac{\mathrm{d}}{\mathrm{d}q^{\prime } }L\left(t,q,q^{\prime } \right)-\frac{\mathrm{d}}{\mathrm{d}q}L\left(t,q,q^{\prime } \right)=0$

eqns = functionalDerivative(-L,[x theta]) == [0;0] % минимизируем функционал

$\begin{array}{l} \left(\begin{array}{c} M\,{\mathrm{e}}^{d\,t} \,\sigma_1 -F_{\textrm{ext}} \,{\mathrm{e}}^{d\,t} +m\,{\mathrm{e}}^{d\,t} \,\sigma_1 +M\,d\,{\mathrm{e}}^{d\,t} \,\frac{\partial }{\partial t}\;x\left(t\right)+d\,m\,{\mathrm{e}}^{d\,t} \,\frac{\partial }{\partial t}\;x\left(t\right)+l\,m\,\sin \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{d\,t} \,{{\left(\frac{\partial }{\partial t}\;\theta \left(t\right)\right)}}^2 -l\,m\,\cos \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{d\,t} \,\sigma_2 -d\,l\,m\,\cos \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{d\,t} \,\frac{\partial }{\partial t}\;\theta \left(t\right)=0\\ m\,{\mathrm{e}}^{d\,t} \,l^2 \,\sigma_3 \,\sigma_2 +m\,{\mathrm{e}}^{d\,t} \,l^2 \,\sigma_4 \,\sigma_2 -m\,{\mathrm{e}}^{d\,t} \,l\,\cos \left(\theta \left(t\right)\right)\,\sigma_1 +d\,m\,{\mathrm{e}}^{d\,t} \,l^2 \,\sigma_3 \,\frac{\partial }{\partial t}\;\theta \left(t\right)+d\,m\,{\mathrm{e}}^{d\,t} \,l^2 \,\sigma_4 \,\frac{\partial }{\partial t}\;\theta \left(t\right)-d\,m\,{\mathrm{e}}^{d\,t} \,l\,\cos \left(\theta \left(t\right)\right)\,\frac{\partial }{\partial t}\;x\left(t\right)-g\,m\,{\mathrm{e}}^{d\,t} \,l\,\sin \left(\theta \left(t\right)\right)=0 \end{array}\right)\\ \mathrm{}\\ \textrm{where}\\ \mathrm{}\\ \;\;\sigma_1 =\frac{\partial^2 }{\partial t^2 }\;x\left(t\right)\\ \mathrm{}\\ \;\;\sigma_2 =\frac{\partial^2 }{\partial t^2 }\;\theta \left(t\right)\\ \mathrm{}\\ \;\;\sigma_3 ={\cos \left(\theta \left(t\right)\right)}^2 \\ \mathrm{}\\ \;\;\sigma_4 ={\sin \left(\theta \left(t\right)\right)}^2 \end{array}$

Приведем систему к размерности первого порядка и составим Handle функцию.

[V,S] = odeToVectorField(eqns); % уменьшаем порядок системы

состояния системы $\left(\begin{array}{c} \theta \\ \mathrm{Dtheta}\\ x\\ \mathrm{Dx} \end{array}\right)$

CartPendf = matlabFunction(V,'Vars',{'t','Y','m','M','l','g','d','F_ext'}); % handle функция

Решаем систему численными методами для следующих параметров системы:

$M=5\;\mathrm{kg},\;m=1\;\mathrm{kg},\;l\;=2\;m,\;g=9\ldotp 81\;\frac{m}{s^2 },\;d=0\ldotp 1\;\frac{1}{s}\ldotp$

Начальное значение угла примем $\theta_0 =180\;\deg$ , внешняя сила $F_{\mathrm{ext}} =0\ldotp 1\;N$ .

init_cond % загрузка начальных условий
F = @(t,Y) CartPendf(t,Y,m,M,l,g,d,0.1); % подстановка параметров в handle функцию
tend = 10; % конец промежутка интегрирования
cond = [pi-deg2rad(theta0); 0; 0; 0]; % начальные условия
opts = odeset('RelTol',1e-6,'AbsTol',1e-6); % настройки точности решателя
Sol = ode45(F,[0 tend],cond,opts); % численное решение системы

Результаты решения нашей системы ДУ:

Решение системы в виде анимации

2. Разработка регулятора (Controller)

2.1 Линеаризация системы

Для разработки контроллера нам потребуется линейная система ДУ в форме пространства состояний

$\dot{x} =A\cdot x+B\cdot u\;\;\;\left(1\right)$

где: $x\left(t\right)\in R^n$ — вектор состояний, $A\;=n\times n$ — матрица состояний, $B=n\times p$ — матрица управления, $u\left(t\right)\in R^p$ — управляющий вектор.

Так как найденная выше ДУ не линейна $\dot{x} =f\left(x,u\right)$ , то требуется её линеаризовать. Проще всего это сделать в окрестности какой-либо фиксированной точки $\bar{x} ,\bar{u}$ , чтобы $f\left(\bar{x} ,\bar{u} \right)=0$ .

Чтобы линеаризовать нашу систему воспользуемся тем наблюдением, что для малой окрестности $\Delta x,\Delta u$ , где $\Delta x=x-\bar{x}$ и $\Delta u=u-\bar{u}$ при разложении функции в ряд Тейлора, ее можно переписать в виде:

$\dot{x} =f\left(x,u\right)\approx f\left(\bar{x} ,\bar{u} \right)+{\frac{\mathrm{d}}{\mathrm{d}x}f\left(x,u\right)|}_{\bar{x} ,\bar{u} } \cdot \Delta x+{\frac{\mathrm{d}}{\mathrm{d}u}f\left(x,u\right)|}_{\bar{x} ,\bar{u} } \cdot \Delta u$

Тогда система примет вид:

$\dot{x} =\frac{\mathrm{d}}{\mathrm{d}t}\left(\bar{x} +\Delta x\right)=\frac{\mathrm{d}}{\mathrm{d}t}\Delta x={\frac{\mathrm{d}}{\mathrm{d}x}f\left(x,u\right)|}_{\bar{x} ,\bar{u} } \cdot \Delta x+{\frac{\mathrm{d}}{\mathrm{d}u}f\left(x,u\right)|}_{\bar{x} ,\bar{u} } \cdot \Delta u$

где $\frac{\mathrm{d}}{\mathrm{d}x}f\left(x,u\right),\frac{\mathrm{d}}{\mathrm{d}u}f\left(x,u\right)$ — Якобианы.

Упрощая запись, систему можно представить в следующем виде: $\Delta \dot{x} =A\cdot \Delta x+B\cdot \Delta u\ldotp$

Иными словами, динамика нашей нелинейной системы в окрестности $\Delta x,\Delta u$ будет равна Якобиану этой системы помноженная на окрестность.

Итак, найдем матрицы и для положения маятника «вверх» и «вниз»:

Vc = feval(symengine,'evalAt',V,'Y = [y1,y2,y3,y4]'); % техническое переименование переменных 
y = sym('y',[4,1]); % вектор символьных переменных
p1 = [0;0;0;0]; % фиксированная точка один - маятник в положении "вверх"
p2 = [pi;0;0;0]; % фиксированная точка два - маятник в положении "вниз"
Df = jacobian(Vc,y); % находим якобиан системы
A1 = subs(Df,y,p1) % подставляем фиксированную точку и находим матрицу А для маятника "вверх"

$\left(\begin{array}{cccc} 0 & 1 & 0 & 0\\ \frac{M\,g+g\,m}{M\,l} & -d & 0 & 0\\ 0 & 0 & 0 & 1\\ \frac{g\,m}{M} & 0 & 0 & -d \end{array}\right)$

A2 = subs(Df,y,p2) % матрица А для маятника в положении "вниз"

$\left(\begin{array}{cccc} 0 & 1 & 0 & 0\\ -\frac{M\,g+g\,m}{M\,l} & -d & 0 & 0\\ 0 & 0 & 0 & 1\\ \frac{g\,m}{M} & 0 & 0 & -d \end{array}\right)$

B1 = subs(diff(Vc,F_ext),y,p1) % матрица B для маятника "вверх"

$\left(\begin{array}{c} 0\\ \frac{1}{M\,l}\\ 0\\ \frac{1}{M} \end{array}\right)$

B2 = subs(diff(Vc,F_ext),y,p2) % матрица B для маятника "вниз"

$\left(\begin{array}{c} 0\\ -\frac{1}{M\,l}\\ 0\\ \frac{1}{M} \end{array}\right)$

Сравним стабильное линейное (маятник в положении «вниз») и не линейное решения для небольшого угла отклонения $\theta_0 =10\;\deg$ .

eqnsL2 = A2*y+B2*F_ext % линейное уравнение для стабильного положения маятника (вниз)

$\left(\begin{array}{c} y_2 \\ -d\,y_2 -\frac{F_{\textrm{ext}} }{M\,l}-\frac{y_1 \,{\left(M\,g+g\,m\right)}}{M\,l}\\ y_4 \\ \frac{F_{\textrm{ext}} }{M}-d\,y_4 +\frac{g\,m\,y_1 }{M} \end{array}\right)$

syms d m M l g
fL1 = matlabFunction(eqnsL2,'Vars',{y,m,M,l,g,d,F_ext}); % handle функция
init_cond % загрузка начальных условий
FL1 = @(~,y) fL1(y,m,M,l,g,d,0); % подстановка начальных условий в линейную системы
FNL1 = @(~,Y) CartPendf(t,Y,m,M,l,g,d,0); % подстановка начальных условий в нелинейную систему
theta0 = 10; % начальный угол
condL = [deg2rad(theta0) 0 0 0]; % начальные условия линейной системы
condNL = [pi-deg2rad(theta0) 0 0 0]; % начальные условия нелинейной системы
SolL1 = ode45(FL1,[0 tend],condL,opts); % решение линейной системы
SolNL1 = ode45(FNL1,[0 tend],condNL,opts); % решение не линейной системы

Сравнение решений линейной и не линейной систем

Можно сказать, что линеаризация прошла успешна, результат нас устраивает.

2.2 Система ДУ в пространстве состояний

Линейная система в форме пространства состояний $\dot{x} =A\cdot x$ очень удобна для анализа, ведь для нее уже известно решение: $x\left(t\right)=e^{A\cdot t} \cdot x\left(0\right)$ .

Продемонстрируем этот факт найдя решение нашей системы в символьном виде:

SymSolL = expm(subs(A2)*t)*condL' % решение системы с помощью матричной экспоненты

$\begin{array}{l} \left(\begin{array}{c} \frac{\pi \,{\left(\frac{\sigma_1 }{2}+\frac{\sigma_2 }{2}+\frac{\sqrt{35}\,\sigma_1 \,\mathrm{i}}{574}-\frac{\sqrt{35}\,\sigma_2 \,\mathrm{i}}{574}\right)}}{18}\\ -\frac{\pi \,{\left(\frac{2943\,\sqrt{35}\,\sigma_1 \,\mathrm{i}}{14350}-\frac{2943\,\sqrt{35}\,\sigma_2 \,\mathrm{i}}{14350}\right)}}{18}\\ -\frac{\pi \,{\left(\frac{\sigma_1 }{6}+\frac{\sigma_2 }{6}-\frac{1}{3}+\frac{\sqrt{35}\,\sigma_1 \,\mathrm{i}}{1722}-\frac{\sqrt{35}\,\sigma_2 \,\mathrm{i}}{1722}\right)}}{18}\\ \frac{\pi \,{\left(\frac{981\,\sqrt{35}\,\sigma_1 \,\mathrm{i}}{14350}-\frac{981\,\sqrt{35}\,\sigma_2 \,\mathrm{i}}{14350}\right)}}{18} \end{array}\right)\\ \mathrm{}\\ \textrm{where}\\ \mathrm{}\\ \;\;\sigma_1 ={\mathrm{e}}^{-\frac{t}{20}-\sigma_3 } \\ \mathrm{}\\ \;\;\sigma_2 ={\mathrm{e}}^{-\frac{t}{20}+\sigma_3 } \\ \mathrm{}\\ \;\;\sigma_3 =\frac{41\,\sqrt{35}\,t\,\mathrm{i}}{100} \end{array}$

Сравним численное и символьное решение

Как и ожидалось, решения совпадают.
Теперь можно предположить, что если мы сможем манипулировать матрицей , то сможем и манипулировать решением нашей системы. Чтобы получать такие решения, какие нам нужны, мы можем использовать управляющий сигнал. Мы можем задать его как $u=-K\cdot x$ , то есть подать состояния системы на вход, создать обратную связь. Здесь — вектор коэффициентов. Подставив это выражение для в выражение (1) , получим систему:

$\dot{x} =A\cdot x+B\cdot \left(-K\cdot x\right)=\left(A-B\cdot K\right)\cdot x$

Видим, что через подбор коэффициентов матрицы , мы можем получить любое нужное нам решение системы при условии, что система полностью управляема.

2.3 Определим устойчивость и управляемость системы

Теперь рассмотрим более подробно нашу линейную систему с маятником в положении «вверх».

Для управления этой системой не плохо знать, является ли она устойчивой. Под термином устойчивости понимается то, что происходит с решениями системы при длительном времени. Если решения системы стремятся к бесконечности — система не устойчива.

Проверяем устойчивость по собственным значениям
матрицы . Если есть хоть одно собственное значение с положительной реальной частью, то система не устойчива. Это можно показать таким образом: матрицу можно записать как комбинацию матрицы собственных значений и собственных векторов : $A=T\cdot D\cdot T^{-1}$ . Тогда разложение в ряд Тейлора матричной экспоненты примет вид:

$e^{A\cdot t} =I+A\cdot t+\frac{A^2 \cdot t^2 }{2!}+\frac{A^3 \cdot t^3 }{3!}+\ldotp \ldotp \ldotp =T\cdot T^{-1} +T\cdot D\cdot T^{-1} \cdot t+\frac{\left(T\cdot D\cdot T^{-1} \cdot T\cdot D\cdot T^{-1} \right)\cdot t^2 }{2!}+\frac{\left(T\cdot D\cdot T^{-1} \cdot T\cdot D\cdot T^{-1} \cdot T\cdot D\cdot T^{-1} \right)\cdot t^3 }{3!}+\ldotp \ldotp \ldotp =T\cdot T^{-1} +T\cdot D\cdot T^{-1} \cdot t+\frac{\left(T\cdot D^2 \cdot T^{-1} \right)\cdot t^2 }{2!}+\frac{\left(T\cdot D^3 \cdot T^{-1} \right)\cdot t^3 }{3!}+\ldotp \ldotp \ldotp =T\cdot \left(I+D\cdot t+\frac{D^2 \cdot t^2 }{2!}+\frac{D^3 \cdot t^3 }{3!}+\ldotp \ldotp \ldotp \right)\cdot T^{-1} =T\cdot e^{D\cdot t} \cdot T^{-1}$

Так как $D=\left\lbrack \begin{array}{cccc} \lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{array}\right\rbrack$ , то $e^{D\cdot t} =\left\lbrack \begin{array}{cccc} e^{\lambda_1 \cdot t} & 0 & \cdots & 0\\ 0 & e^{\lambda_2 \cdot t} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e^{\lambda_n \cdot t} \end{array}\right\rbrack$ , где $\lambda_1 ,\lambda_2 ,\ldotp \ldotp \ldotp ,\lambda_n$ — собственные значения матрицы .

Из этого выражения видно, что собственные числа с положительной реальной частью приводят к бесконечному экспоненциальному росту решения, так как:

$e^{\lambda \cdot t} =e^{\left(a+i\cdot b\right)\cdot t} =e^{a\cdot t} \cdot \left(\cos \left(b\cdot t\right)+i\cdot \sin \left(b\cdot t\right)\right)$

Если a>0» src=«https://habrastorage.org/getpro/habr/upload_files/584/dba/c97/584dbac970d889696899f7f60330a1fe.svg» />, то экспоненциальный рост, если <img alt= то затухание.

Итак, проверим на устойчивость нашу систему. Найдем собственные значения матрицы .

A = double(subs(A1)); % матрица состояний системы
eig(A) % найдем собственные значения
ans = 4×1
         0
   -0.1000
    2.3766
   -2.4766

Видим, что есть положительные корни, что ожидаемо. Делаем вывод, что система не устойчива.
Теперь определим можем ли мы управлять нашей системой с помощью управляющего сигнала .

Воспользуемся теоремой Кели-Гамильтона, которая гласит, что матрица удовлетворяет собственному характеристическому уравнению $\det \left(A-\lambda \cdot I\right)=0$ .

$\lambda^n +a_{n-1} \cdot \lambda^{n-1} +\ldotp \ldotp \ldotp +a_1 \cdot \lambda +a_0 =0$ — характеристическое уравнение

$A^n +a_{n-1} \cdot A^{n-1} +\ldotp \ldotp \ldotp +a_1 \cdot A+a_0 \cdot I=0$ — удовлетворяющее матрицей уравнение

$A^n ={-a}_0 \cdot I-a_1 \cdot A-\ldotp \ldotp \ldotp -a_{n-1} \cdot A^{n-1}$ — выразим старшую степень матрицы .

Тогда, используя тот факт, что аналитическая функция $f\left(A\right)=r\left(A\right)=\sum_{k=0}^{n-1} c_k \cdot A^k$ матричную экспоненту можно записать в конечном виде:

$e^{A\cdot t} =\varphi_0 \left(t\right)\cdot I+\varphi_1 \left(t\right)\cdot A+\varphi_2 \left(t\right)\cdot A^2 +\ldotp \ldotp \ldotp +\varphi_{n-1} \left(t\right)\cdot A^{n-1} \;\;\;\left(2\right)$

Решение системы $\xi$ , которого мы хотим добиться равно:

$\xi =\int_0^t e^{A\cdot \left(t-\tau \right)} Bu\left(\tau \right)d\tau$

Подставим в это выражение, выражение (2) :

$\xi =\int_0^t \left(\varphi_0 \left(t-\tau \right)u\left(\tau \right)IB+\varphi_1 \left(t-\tau \right)u\left(\tau \right)AB+\varphi_2 \left(t-\tau \right){u\left(\tau \right)A}^2 B+\ldotp \ldotp \ldotp +\varphi_{n-1} \left(t-\tau \right)u\left(\tau \right)A^{n-1} B\right)d\tau =B\int_0^t \varphi_0 \left(t-\tau \right)u\left(\tau \right)d\tau +AB\int_0^t \varphi_1 \left(t-\tau \right)u\left(\tau \right)d\tau +\ldotp \ldotp \ldotp +A^{n-1} B\int_0^t \varphi_{n-1} \left(t-\tau \right)u\left(\tau \right)d\tau$ $\xi =\left\lbrack \begin{array}{cccc} B & AB & \cdots & A^{n-1} B \end{array}\right\rbrack \left\lbrack \begin{array}{c} \int_0^t \varphi_0 \left(t-\tau \right)u\left(\tau \right)d\tau \\ \int_0^t \varphi_1 \left(t-\tau \right)u\left(\tau \right)d\tau \\ \vdots \\ \int_0^t \varphi_{n-1} \left(t-\tau \right)u\left(\tau \right)d\tau \end{array}\right\rbrack$

Матрица $Co=\left\lbrack \begin{array}{ccccc} B & AB & A^2 B & \cdots & A^{n-1} B \end{array}\right\rbrack$ называется матрицей управляемости. Это выражение говорит нам, что если матрица управляемости имеет ранг , то есть охватывает все состояния системы, то мы можем достичь любого нужного нам решения $\xi$ с помощью управления .

Проверим управляемость нашей системы.

B = double(subs(B1)); % матрица управления системы
rank(ctrb(A,B)) % найдем ранг матрицы управляемости
ans = 4

Ранг равен 4, и порядок системы равен 4, значит система полностью управляема.

2.4 Расчет регулятора методом размещения полюсов (модальный синтез)

Теперь можно приступить к процессу расчета регулятора и управлению системой.

Стабилизируем систему, изменив собственные числа с
помощью обратной связи и матрицы усиления . Пусть новые собственные числа будут равны -1.1, -1.2, -1.3, -1.4.

p = [-1.1; -1.2; -1.3; -1.4]; % желаемые собственные числа системы

Тогда матрица будет иметь вид:

K = place(A,B,p) % матрица усиления K
K = 1×4
  152.3579   61.9939   -2.4489   -6.9969

Пусть начальное положение тележки равно -2, а мы потребуем, чтобы она переместилась в положение 2.

Промоделируем систему с обратной связью и посмотрим
результаты

Sdes = [0;0;2;0]; % желаемые состояния системы
cond = [0;0;-2;0]; % начальные условия
F2 = @(t,Y) CartPendf(t,Y,m,M,l,g,d,-K*(Y-Sdes)); % нелинейная система с обратной связью
Sol2 = ode45(F2,[0 tend],cond,opts); % решение системы

Видим, что система отрабатывает наши требования.

Решение системы в виде анимации

2.5 Расчет регулятора методом оптимального управления (LQR)

Мы разместили полюса системы произвольно, но теперь
хотелось бы повысить эффективность управления. Хочется тратить поменьше энергии
на перемещения, но получать побольше скорость. Один из способов это сделать,
рассчитать линейный квадратичный регулятор (LQR). Идея заключается в
минимизации функции потерь:

$J=\int_0^{\infty } \left(x^T Qx+u^T Ru\right)dt$

где: $Q=n\times n$ — матрица, которая показывает, насколько медленно состояние должно сходиться к тому, которое требуется, и $R=p\times p$ — матрица стоимости энергии, которая показывает, насколько дорого обходится движение.

Найдем такой вектор , чтобы закон управления $u=-K\cdot x$ минимизировал функцию потерь лучшим образом.

Q = diag([1 0.1 2 0.1]); % матрица стоимости состояний
R = 0.01; % матрица стоимости энергии
K = lqr(A,B,Q,R) % расчет матрицы усиления
K = 1×4
  274.7147  116.8560  -14.1421  -23.6448

Промоделируем систему

F3 = @(t,Y) CartPendf(t,Y,m,M,l,g,d,-K*(Y-Sdes)); % нелинейная система с обратной связью
Sol3 = ode45(F3,[0 tend],cond,opts); % решение системы

Как видно из графиков, маятник принял требуемое положение заметно быстрее.

Решение системы в виде анимации

2.6 Наблюдаемость системы

Наш регулятор, рассчитанный выше, требует для работы измерения всех состояний системы, но в реальности далеко не всегда есть такая возможность. Система в пространстве состояний, которая оценивает не все состояния записывается в следующем виде:

$\begin{array}{l} \dot{x} =A\cdot x+B\cdot u\\ y=C\cdot x \end{array}$

где: $y\in R^q$ — вектор выхода, $C=q\times n$ — матрица выхода.

По аналогии с управляемостью, можно ввести термин наблюдаемости, который скажет нам, сможем ли мы получить полную оценку состояний системы, с помощью доступных измерений. Здесь действуют аналогичные рассуждения, что и для понятия управляемости, только с транспонированием.

$Ob=\left\lbrack C\;AC\;A^2 C\cdots A^{n-1} C\right\rbrack$

В нашей системе легко измерить только состояния и $\theta$ , поэтому запишем следующую матрицу :

C = [1 0 0 0; 0 0 1 0]; % матрица выхода

Оценим наблюдаемость нашей системы:

rank(obsv(A,C)) % найдем ранг матрицы наблюдаемости 
ans = 4

Ранг равен порядку системы значит она наблюдаема. Можно управлять нашей линейной системой только по состоянию , но для применения в нелинейной системе проще иметь и $\theta$ .

Итак, наша система наблюдаема, но регулятору требуются все состояния. И тут встает необходимость разработать наблюдателя, или оценщика системы. Этим оценщиком у нас будет фильтр Калмана.
Про фильтр Калмана есть множество литературы, мы же кратко опишем его идею.
Зная динамику системы (матрицу ), мы можем составить линейную модель, входом которой будут измеренные состояния и входной сигнал , а выходом полный вектор состояний системы $\hat{x}$ :

$\begin{array}{l} \frac{\mathrm{d}}{\mathrm{d}t}\hat{x} =A\cdot \hat{x} +B\cdot u+K_f \cdot \left(y-\hat{y} \right)\\ \hat{y} =C\cdot \hat{x} \end{array}$

где: $\hat{x}$ — оценка состояний системы, K_f — матрица усиления фильтра.

Каждое полученное измерение сравнивается с измерениями, которые предсказаны фильтром $\hat{y}$ и если есть разница, то полное состояние $\hat{x}$ корректируется в соответствие с матрицей K_f .

Если мы вычислим ошибку $\varepsilon =x-\hat{x}$ , то

$\frac{\mathrm{d}}{\mathrm{d}t}\varepsilon =\frac{\mathrm{d}}{\mathrm{d}t}x-\frac{\mathrm{d}}{\mathrm{d}t}\hat{x} =Ax+Bu-A\hat{x} -K_f C\hat{x} -K_f y-Bu=A\left(x-\hat{x} \right)-K_f C\left(x-\hat{x} \right)=\left(A-K_f C\right)\varepsilon$

из чего можно сделать вывод, что ошибка между полным состоянием системы и оцененным состоянием может быть нулем, если система наблюдаема. Иными словами, с помощью матрицы K_f мы можем разместить собственные числа для системы ошибки там, где захотим, и получить любую точность.
Но в реальной системе существуют помехи и шумы, поэтому мы должны найти такую матрицу K_f , чтобы функция потерь $J=E\left\lbrack {\left(x-\hat{x} \right)}^T \left(x-\hat{x} \right)\right\rbrack$ (мат. ожидание ошибки) оказалась минимальной.
С помощью MATLAB спроектировать оценщик состояний довольно просто:

Q = [0.7164; 1.2793; 0.7659; 2.3542].*eye(4); % матрица помех
R = [0.0125;0.7620].*eye(2); % матрица шума

Получим матрицу K_f :

[Kf,~,~] = lqe(A,eye(4),C,Q,R) % расчет вектора усиления фильтра
Kf = 4×2
    9.5200    0.0061
   16.6607    0.0267
    0.3708    2.0365
    2.6577    1.5723

Составим матрицы оценщика:

KA = A-Kf*C; % матрица А фильтра
KB = [B Kf]; % матрица B фильтра
KC = eye(4); % матрица C фильтра
KD = 0*[B Kf]; % матрица D фильтра

Составим полную систему уравнений с нелинейным маятником, оценщиком и регулятором. Так же добавим шум к измерениям. Потребуем, чтобы из положения x_0 =0 , маятник попал в положение x=2 .

syms theta_kf(t) x_kf(t) w1 w2 % дополнительные символьные переменные
Sdes = [0;0;2;0]; % требуемое конечное состояние
eqns1 = subs(eqns); % подстановка параметоров системы
eqns1 = subs(eqns1,F_ext,K*(Sdes-[theta_kf;diff(theta_kf);x_kf;diff(x_kf)])); % нелинейная система
eqns2 = diff([theta_kf;diff(theta_kf);x_kf;diff(x_kf)]) == KA*[theta_kf;diff(theta_kf);x_kf;diff(x_kf)] + KB*[K*(Sdes-[theta_kf;diff(theta_kf);x_kf;diff(x_kf)]);theta+w1;x+w2]; % оценщик
eqnsC = vpa([eqns1;eqns2],3) % итоговая СДУ

$\begin{array}{l} \left(\begin{array}{c} {\mathrm{e}}^{0.1\,t} \,{\left(275.0\,\theta_{\textrm{kf}} \left(t\right)-14.1\,x_{\textrm{kf}} \left(t\right)+117.0\,\frac{\partial }{\partial t}\;\theta_{\textrm{kf}} \left(t\right)-23.6\,\frac{\partial }{\partial t}\;x_{\textrm{kf}} \left(t\right)+28.3\right)}+6.0\,{\mathrm{e}}^{0.1\,t} \,\sigma_4 +0.6\,{\mathrm{e}}^{0.1\,t} \,\frac{\partial }{\partial t}\;x\left(t\right)-0.2\,\cos \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{0.1\,t} \,\frac{\partial }{\partial t}\;\theta \left(t\right)+2.0\,\sin \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{0.1\,t} \,{{\left(\frac{\partial }{\partial t}\;\theta \left(t\right)\right)}}^2 -2.0\,\cos \left(\theta \left(t\right)\right)\,{\mathrm{e}}^{0.1\,t} \,\sigma_1 =0.0\\ 4.0\,{\mathrm{e}}^{0.1\,t} \,\sigma_2 \,\sigma_1 -2.0\,{\mathrm{e}}^{0.1\,t} \,\cos \left(\theta \left(t\right)\right)\,\sigma_4 +4.0\,{\mathrm{e}}^{0.1\,t} \,\sigma_3 \,\sigma_1 +0.4\,{\mathrm{e}}^{0.1\,t} \,\sigma_2 \,\frac{\partial }{\partial t}\;\theta \left(t\right)-0.2\,{\mathrm{e}}^{0.1\,t} \,\cos \left(\theta \left(t\right)\right)\,\frac{\partial }{\partial t}\;x\left(t\right)+0.4\,{\mathrm{e}}^{0.1\,t} \,\sigma_3 \,\frac{\partial }{\partial t}\;\theta \left(t\right)-19.6\,{\mathrm{e}}^{0.1\,t} \,\sin \left(\theta \left(t\right)\right)=0.0\\ \frac{\partial }{\partial t}\;\theta_{\textrm{kf}} \left(t\right)=\frac{\partial }{\partial t}\;\theta_{\textrm{kf}} \left(t\right)+9.52\,w_1 +0.00608\,w_2 +9.52\,\theta \left(t\right)-9.52\,\theta_{\textrm{kf}} \left(t\right)+0.00608\,x\left(t\right)-0.00608\,x_{\textrm{kf}} \left(t\right)\\ \frac{\partial^2 }{\partial t^2 }\;\theta_{\textrm{kf}} \left(t\right)=16.7\,w_1 +0.0267\,w_2 +16.7\,\theta \left(t\right)-38.2\,\theta_{\textrm{kf}} \left(t\right)+0.0267\,x\left(t\right)+1.39\,x_{\textrm{kf}} \left(t\right)-11.8\,\frac{\partial }{\partial t}\;\theta_{\textrm{kf}} \left(t\right)+2.36\,\frac{\partial }{\partial t}\;x_{\textrm{kf}} \left(t\right)-2.83\\ \frac{\partial }{\partial t}\;x_{\textrm{kf}} \left(t\right)=\frac{\partial }{\partial t}\;x_{\textrm{kf}} \left(t\right)+0.371\,w_1 +2.04\,w_2 +0.371\,\theta \left(t\right)-0.371\,\theta_{\textrm{kf}} \left(t\right)+2.04\,x\left(t\right)-2.04\,x_{\textrm{kf}} \left(t\right)\\ \frac{\partial^2 }{\partial t^2 }\;x_{\textrm{kf}} \left(t\right)=2.66\,w_1 +1.57\,w_2 +2.66\,\theta \left(t\right)-55.6\,\theta_{\textrm{kf}} \left(t\right)+1.57\,x\left(t\right)+1.26\,x_{\textrm{kf}} \left(t\right)-23.4\,\frac{\partial }{\partial t}\;\theta_{\textrm{kf}} \left(t\right)+4.63\,\frac{\partial }{\partial t}\;x_{\textrm{kf}} \left(t\right)-5.66 \end{array}\right)\\ \mathrm{}\\ \textrm{where}\\ \mathrm{}\\ \;\;\sigma_1 =\frac{\partial^2 }{\partial t^2 }\;\theta \left(t\right)\\ \mathrm{}\\ \;\;\sigma_2 ={\cos \left(\theta \left(t\right)\right)}^2 \\ \mathrm{}\\ \;\;\sigma_3 ={\sin \left(\theta \left(t\right)\right)}^2 \\ \mathrm{}\\ \;\;\sigma_4 =\frac{\partial^2 }{\partial t^2 }\;x\left(t\right) \end{array}$

[Vkf,Skf] = odeToVectorField(eqnsC); % уменьшим порядок системы до первого
PendControl = matlabFunction(Vkf,'Vars',{'t','Y','w1','w2'}); % составим hendle функцию

Решим полную систему

w1 = @(x) rand/100; % шум
tend = 10; % конечное время
cond = zeros(8,1); % начальные условия

pfig = figure;
psub1 = subplot(2,1,1); grid on; psub1.Subtitle.String = 'theta with noise';
psub2 = subplot(2,1,2); grid on; psub2.Subtitle.String = 'x with noise';
Alh1 = animatedline('Parent',psub1,'Color','r');
Alh2 = animatedline('Parent',psub2,'Color','b');
PendControlF = @(t,y) odefcnintdisp(t,y,PendControl,w1(t),w1(t),Alh1,Alh2); % подставим шум в функцию
Sol4 = ode45(PendControlF,[0 tend],cond); % решим систему

Результаты решения итоговой системы ДУ

Решение системы в виде анимации

В результате получена модель перевернутого маятника.

Ссылка на проект

Ссылка на лекции Steve Brunton, по которым написана статья