Как быстро и безболезненно выбрать лучшую из десяти выборок27.04.2024 10:00

Всем привет! Меня зовут Мария Ходякова, я продуктовый аналитик Тинькофф Страхования. В этой статье мы поговорим о множественном тестировании. Хорошо известен такой подход, как А/В-тестирование, когда в тесте участвуют две выборки. Но иногда нужно сравнить больше двух выборок и определить статистически значимо лучшую. Например, найти среди пяти баннеров в приложении лучший по конверсии продаж. Именно для этого и нужно множественное тестирование.

Статья имеет следующую структуру. Сначала описывается математическая постановка задачи и наиболее простой путь ее решения. Далее мы переходим к тому, как можно решить данную задачу более хитрым способом, существенно сократив размер данных, необходимых для тестирования.

В конце статьи также приводится библиотека с функциями для множественного тестирования по описанному алгоритму, реализованному на языке Python.

Длительность теста и постановка задачи

На идейном уровне множественное тестирование отличается от А/В только количеством выборок. Существенные различия скрываются на статистическом уровне. До начала теста нужно определить статистический критерий и минимальный размер выборки для получения стат. значимого результата. Минимальный размер считается по

уровню значимости и мощности — обычно и $80\%$ соответственно;
минимальному детектируемому эффекту MDE, или минимальному отклонению, которое хотим зафиксировать для метрики на выборках;
теоретической оценке дисперсии метрики, которая вычисляется по историческим данным;
отношению размеров выборок друг к другу.

При А/В-тесте этап определения критерия и выбора минимального размера не сильно чувствуется, поскольку создано много калькуляторов. Нам только нужно указать соответствующие параметры для нашего теста.

При множественном тестировании этап определения критерия и выбора минимального размера самый сложный. Если об этом совсем не подумать, может быть повышена вероятность ошибки. Если вникнуть, размер выборки может стать заоблачным, что отрицательно повлияет на длительность теста.

Разберемся с вычислением минимального размера выборки и возможными критериями для множественного тестирования как с идейной, так и с математической стороны.

Статистическая постановка задачи: определить лучшую из выборок по целевой метрике (к примеру, конверсии). Здесь под лучшей выборкой понимается та, что дает наибольшее среднее значение целевой метрики. Сформулируем задачу статистически в случае выборок равного размера.

Пусть $X_{1,i}, \dotsc, X_{n,i} \sim F_i, i \in \{1, \dotsc, k\},$ где $F_i \in \mathcal{F}, \mathcal{F}$ — множество возможных распределений. К примеру, в случае теста конверсий есть множество распределений Бернулли с различными параметрами $p \in [0, 1]$ . Пусть $\mathbf{E} X_{1,i} = \mu_i$ — математическое ожидание, или среднее значение, $X_{1,i}, \mathbf{D} X_{1,i} = \sigma_i^2 \in (0, \infty)$ — дисперсия $X_{1,i}$ . Предположим, что случайные величины $X_{j,i}, j \leq n, i \leq k,$ независимы в совокупности.

Тест, основанный на попарных сравнениях

Мы проверяем нулевую гипотезу H_0 против гипотез вида

$H_i: \mu_i > \max\{\mu_1, \dotsc, \mu_{i-1}, \mu_{i+1}, \dotsc, \mu_k\}, \quad i = 1, \dotsc, k.» src=«https://habrastorage.org/getpro/habr/upload_files/c7d/0d4/dfc/c7d0d4dfc52ee287e2a68f03187e86c6.svg» /> То есть <img alt=$ утверждает невыполнение остальных гипотез.

Так, если на -й выборке будет статистически наибольшее среднее значение целевой метрики, то мы примем гипотезу H_i . Иначе будет принята гипотеза H_0 . В примере с баннерами гипотеза H_i означает, что -й баннер имеет наибольшую конверсию продажи, H_0 — все баннеры дают одинаковую конверсию продажи.

Отметим, что при k=2 получаем следующие классические гипотезы:

$H_0: \mu_1 = \mu_2, \quad H_1: \mu_1 > \mu_2, \quad H_2: \mu_2 > \mu_1,» src=«https://habrastorage.org/getpro/habr/upload_files/24e/d57/f85/24ed57f8541c62bb3908631587822c8a.svg» /> где <img alt=$ предполагает равенство средних значений целевой метрики на обеих выборках, H_1 и H_2 — преобладание целевой метрики на первой и второй выборках соответственно.

Один из вариантов определения лучшей выборки — сравнение выборок попарно. То есть мы проводим C_k^2 = k (k-1) / 2 А/В-тестов. К примеру, при k=10 нужно провести сравнений. Кажется, выглядит пугающе. Выясним, даст ли это желаемый результат.

Размер одной выборки и построение критерия. Пусть заданы $\alpha, \beta \in (0, 1)$ — уровень значимости и вероятность ошибки второго рода соответственно, d>0» src=«https://habrastorage.org/getpro/habr/upload_files/f9c/c34/b49/f9cc34b491f8faeef9f353bea35fb366.svg» /> — MDE. Выберем <img alt= для случая двух выборок с односторонней проверкой гипотезы по формуле:

$n = \frac{2 \max_i{\sigma_i^2}}{\widetilde{d}^2} (z_{1-\widetilde{\alpha}} - z_{\widetilde{\beta}})^2,$

где $z_\gamma$ — $\gamma$ -квантиль стандартного нормального распределения, уровень значимости $\widetilde{\alpha} = \alpha / k,$ вероятность ошибки второго рода $\widetilde{\beta} = \beta / (k-1),$ минимальный детектируемый эффект $\widetilde{d} = d$ . Тогда — минимальный размер выборки для каждой из вариаций.

Доказательство

Критерий $\varphi(x),$ где $x = (x_{i,j}, i \leq n, j \leq k),$ будет сопоставлять верную гипотезу, то есть $\varphi \in \{0, \ldots, k\}$ .

Составим односторонние гипотезы $H_{i > j}: \mu_i > \mu_j» src=«https://habrastorage.org/getpro/habr/upload_files/06d/841/42d/06d84142d24bd16a495e36f8a15129c9.svg» /> и <img alt=$ . Будем предполагать, что для проверки односторонних гипотез используется такая статистика $T_{i,j} = - T_{j,i},$ что в случае $\mu_i > \mu_j» src=«https://habrastorage.org/getpro/habr/upload_files/420/6a3/4e0/4206a34e0eb5c608fd1a36a5956762d7.svg» /> она принимает большие по модулю положительные значения, в случае <img alt=$ она принимает большие по модулю отрицательные значения.

Положим

$D_{i < j} = \left\{T_{i,j} < t_{\widetilde{\alpha}}\right\}, \quad D_{i > j} = \left\{T_{i, j} > t_{1-\widetilde{\alpha}}\right\},» src=«https://habrastorage.org/getpro/habr/upload_files/450/01f/f31/45001ff310d264580d68fd509faa710b.svg» />где <img alt=$ — число, которое мы выберем по уровню значимости $\alpha$ позднее, $t_\gamma$ — $\gamma$ -квантиль предельного распределения статистики $T_{i,j}$ при гипотезе H_0

. Если мы проверяем H_0

против $H_{i > j}» src=«https://habrastorage.org/getpro/habr/upload_files/766/ee9/082/766ee9082b713172e07b19f10fe2be0a.svg» /> или <img alt=$ вероятность ошибки первого рода такого критерия будет равна $\widetilde{\alpha},$ причем в случае ненулевой гипотезы мы можем утверждать стат. значимо об отличии $\mu_i$ от $\mu_j$ в одну или другую сторону.

Логично положить $\varphi(x) = j,$ если

$T_{j,1}(x) > t_{1-\widetilde{\alpha}}, \ldots, T_{j, k}(x) > t_{1-\widetilde{\alpha}},» src=«https://habrastorage.org/getpro/habr/upload_files/5ec/cc9/30b/5eccc930b42c12649adbdc24a380111c.svg» />то есть имеет место событие <img alt=$ 1} \cap \ldots \cap D_{j > k}» src=«https://habrastorage.org/getpro/habr/upload_files/bf9/14a/879/bf914a87976c555108ccf4fb17a87261.svg» />. При этом события $\{\varphi=j\}$ не пересекаются. Если ни для какого $j \in \{1, \ldots, k\}$ условие не выполнено, полагаем $\varphi(x)=0$ .

Можно посчитать вероятность ошибки первого рода критерия

$\mathbf{P}_{H_0}(\varphi > 0) = \sum_{j=1}^k \mathbf{P}_{H_0}(\varphi = j) = \sum_{j=1}^k \mathbf{P}_{H_0}\left (D_{j > 1} \cap \ldots \cap D_{j > k}\right) \leq \\ \leq \sum_{j=1}^k \min_i\left\{\mathbf{P}_{H_0}(D_{j > i}) \mid j \neq i\right\} \approx \sum_{j=1}^k \widetilde{\alpha} = \widetilde{\alpha} k = \alpha.» src=«https://habrastorage.org/getpro/habr/upload_files/e33/98f/4f1/e3398f4f1ae3a967d00c79926ec22dac.svg» />Для подсчета размера выборки нужно зафиксировать MDE, равное <img alt=$ , и вероятность ошибки второго рода, равную $\beta$ . Пусть

размер выборки в каждой группе, был выбран так, чтобы вероятность ошибки второго рода при проверке H_0

против $\widetilde{H}_{i > j}: \mu_i = \mu_j + d» src=«https://habrastorage.org/getpro/habr/upload_files/dc2/fba/1a5/dc2fba1a5ebf62bce2d6441dbb166157.svg» /> или <img alt=$ была равна $\widetilde{\beta}$ . Вообще говоря,

может зависеть от

поэтому мы выберем максимальный из всех комбинаций. Рассмотрим $\widetilde{H}_j: \mu_j = \mu_1 + d = \ldots = \mu_k + d$ . Тогда

$\mathbf{P}_{\widetilde{H}_j}(\varphi \neq j) = \mathbf{P}_{\widetilde{H}_j}\left(\overline{D}_{j > 1} \cup \ldots \cup \overline{D}_{j > k}\right) \leq \\ \leq \sum_{i \neq j} \mathbf{P}_{\widetilde{H}_j}\left (\overline{D}_{j > i}\right) = (k — 1) \widetilde{\beta} = \beta.» src=«https://habrastorage.org/getpro/habr/upload_files/466/8f9/637/4668f9637e024c3a7812da22110c618c.svg» />Таким образом, выбрав <img alt=$ так, чтобы при проверке $H_{i = j}: \mu_i = \mu_j$ против $\widetilde{H}_{i > j}: \mu_i = \mu_j + d» src=«https://habrastorage.org/getpro/habr/upload_files/57c/3b4/b82/57c3b4b82d89870386eb454a6068db04.svg» /> или <img alt=$ вероятность ошибок первого и второго рода не превосходила соответственно $\alpha/k$ и $\beta/(k-1),$ мы сможем стат. значимо обнаружить отклонение максимума порядка

с вероятностью ошибок первого и второго рода, не превосходящей $\alpha$ и $\beta$ соответственно.

Что и требовалось доказать.

При множественном тестировании выборок с уровнем значимости $\alpha$ и вероятностью ошибки второго рода $\beta,$ сравнивая попарно выборки, мы проводим C_k^2 А/В-тестов с уровнем значимости $\alpha/k$ и вероятностью ошибки второго рода $\beta/(k-1)$ . Если некоторая -я выборка стат. значимо лучше каждой другой выборки, принимается гипотеза H_i, где $i=1,\dotsc,k,$ иначе принимается гипотеза H_0 . Математически критерий теста описан в доказательстве.

Выбранное решение не самое простое. Без каких-либо доказательств мы могли прийти к тому, что можно провести C_k^2 попарных сравнений с уровнем значимости $\alpha/C_k^2$ и вероятностью ошибки второго рода $\beta/(C_k^2-1)$ .

Моделирование. Мы провели математический разбор критерия, основанного на попарных сравнениях, который будем называть простым решением. Но что это даст на практике? Чтобы с этим разобраться, обратимся к моделированию.

Мы не хотим ошибаться слишком часто, следовательно, мы будем контролировать вероятность ошибки первого рода, то есть вероятность отклонить нулевую гипотезу при ее справедливости. Величина эта теоретическая, поэтому мы промоделируем частоту неверного отклонения нулевой гипотезы, близкую к истинной вероятности ошибки первого рода при достаточном количестве моделирований. Для примера используем распределение Бернулли, как в случае с тестом конверсии.

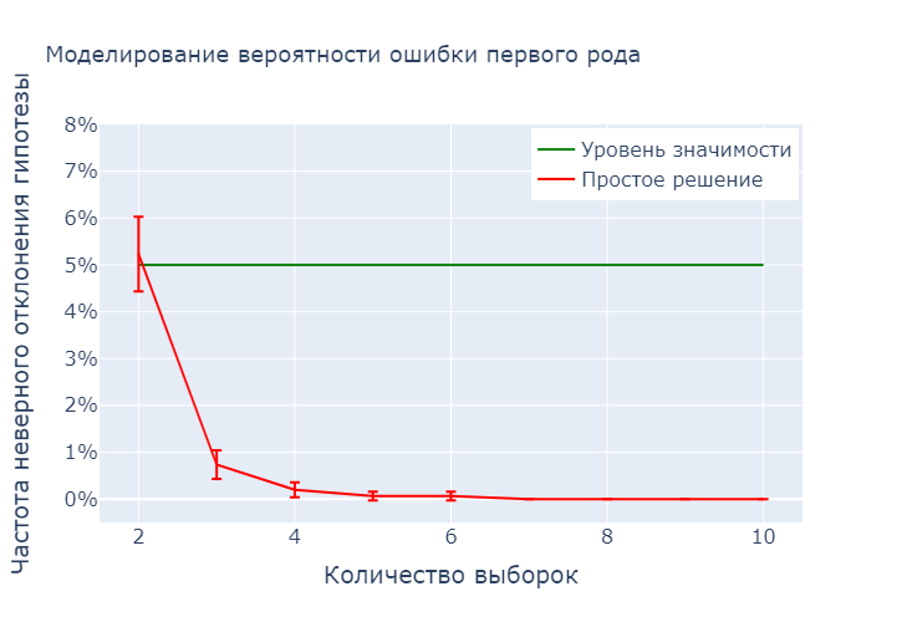
При увеличении количества выборок частота неверного отклонения нулевой гипотезы быстро убывает к нулю. Для нас это плохо, поскольку у нас нет цели быть слишком осторожными. Мы заложили уровень значимости 5% и хотим оставаться на этом уровне.

Возникает вопрос: на что влияет наша чрезмерная осторожность? Посмотрим на минимальный размер одной выборки в зависимости от количества выборок.

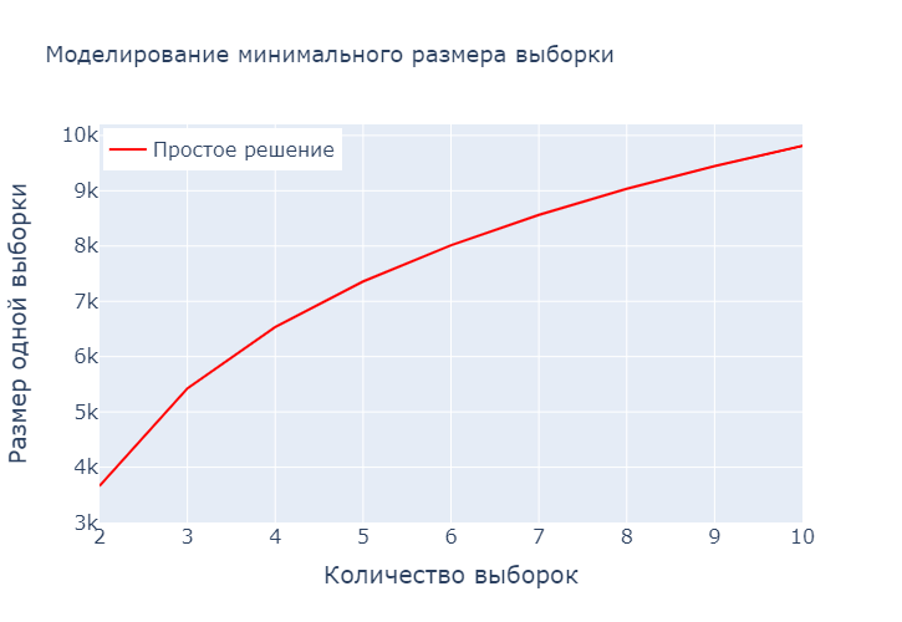
Близкая к нулю частота неверного отклонения нулевой гипотезы влияет на размер одной выборки. Минимальный размер растет при увеличении количества выборок, что сильно скажется на длительности теста.

Решение нас не устраивает, поэтому углубимся в теорию и придумаем другое.

Тест, основанный на предельном сравнении

Мы проверяем гипотезу

$H_0: \mu_1 = \dotsc = \mu_k$

против гипотез вида

$H_i: \mu_i > \max\{\mu_1, \dotsc, \mu_{i-1}, \mu_{i+1}, \dotsc, \mu_k\}, \quad i = 1, \dotsc, k.» src=«https://habrastorage.org/getpro/habr/upload_files/41c/f79/8a4/41cf798a47280619c56ed3c7ab8708c7.svg» /> Отметим, что гипотезы в совокупности не дают все возможные события. К примеру, не рассматриваются события, что существуют такие <img alt=$ что $\mu_i = \mu_j = \max\{\mu_1, \ldots, \mu_k\}$ и все средние не равны.

Снова прокомментируем это на примере с баннерами. Гипотеза H_j означает, что -й баннер дает наибольшую конверсию продажи и она больше конверсии на других баннерах, H_0 — все баннеры дают одинаковую конверсию продажи. Но возможен случай, что есть два баннера, которые дают одинаковую конверсию продажи и их конверсия максимальна. Принятие нулевой гипотезы H_0 означает не ее верность, неверность остальных гипотез.

Размер одной выборки и построение критерия. Пусть выборки имеют одинаковый размер, заданы уровень значимости $\alpha,$ вероятность ошибки второго рода $\beta$ и минимальное отклонение . Тогда в общем случае для получения минимального размера выборки можно использовать метод Монте-Карло для моделирования квантилей распределений случайных величин

$\min_{i, i \neq j} \left\{\frac{Z_j}{\sqrt{1 + \frac{\sigma_i^2}{\sigma_j^2}}} - \frac{Z_i}{\sqrt{1 + \frac{\sigma_j^2}{\sigma_i^2}}} \right\}, \quad j = 1, \dotsc, k,$

где Z_j — независимые случайные величины со стандартным нормальным распределением.

Для снижения вычислительной сложности алгоритма выделим частный случай равных дисперсий при нулевой гипотезе $\sigma_1^2 = \dotsc = \sigma_k^2 = \sigma^2$ на всех выборках, который наиболее часто встречается на практике (к примеру, тест конверсии). При $\alpha, \beta \in (0, 1), d > 0» src=«https://habrastorage.org/getpro/habr/upload_files/b6b/36b/90d/b6b36b90dbaa6e2c5ef6ed4c090cdc77.svg» /> размер выборки определяется равенством <img alt=$

где $c_\gamma$ — $\gamma$ -квантиль распределения случайной величины

$\frac{1}{\sqrt{2}} \min_i \left\{Z_1 - Z_i | i \neq 1\right\}.$ Доказательство

Пусть критерий $\varphi(x),$ где $x = (x_{i,j}, i \leq n, j \leq k),$ будет сопоставляться набору выборок номер гипотезы следующим образом. Если $\varphi(x) = j, j \neq 0,$ верна гипотеза H_j . Если $\varphi(x)=0,$ ни одна из гипотез $H_j, j = 1, \dotsc, k,$ не верна.

Составим односторонние гипотезы $H_{i > j}: \mu_i > \mu_j» src=«https://habrastorage.org/getpro/habr/upload_files/ccf/e60/80e/ccfe6080e304147131310f1270d960ec.svg» /> и <img alt=$ . Будем предполагать, что для проверки односторонних гипотез используется такая статистика $T_{i,j} = - T_{j,i},$ что в случае $\mu_i > \mu_j» src=«https://habrastorage.org/getpro/habr/upload_files/b62/252/47e/b6225247ec4e60aec5f750ad7d2160dc.svg» /> она принимает большие по модулю положительные значения, в случае <img alt=$ она принимает большие по модулю отрицательные значения.

Положим

$D_{i < j} = \left\{T_{i,j} < t_{\widetilde{\alpha}}\right\}, \quad D_{i > j} = \left\{T_{i, j} > t_{1-\widetilde{\alpha}}\right\},» src=«https://habrastorage.org/getpro/habr/upload_files/984/eb3/3e4/984eb33e44ba67d491ba19181c3181b1.svg» />где <img alt=$ — число, которое мы выберем по уровню значимости $\alpha$ позднее, $t_\gamma$ — $\gamma$ -квантиль предельного распределения статистики $T_{i,j}$ при гипотезе H_0

. Если мы проверяем H_0

против $H_{i > j}» src=«https://habrastorage.org/getpro/habr/upload_files/bb6/b2e/75a/bb6b2e75ac12c7bb320e22579655a131.svg» /> или <img alt=$ вероятность ошибки первого рода такого критерия будет равна $\widetilde \alpha,$ причем в случае ненулевой гипотезы мы можем утверждать стат. значимо об отличии $\mu_i$ от $\mu_j$ в одну или другую сторону.

Логично положить $\varphi(x)=j,$ если

$T_{j,1}(x) > t_{1-\widetilde{\alpha}}, \ldots, T_{j, k}(x) > t_{1-\widetilde{\alpha}}.» src=«https://habrastorage.org/getpro/habr/upload_files/929/33c/6cc/92933c6cc0622431776e16ed8919933a.svg» />Если <img alt=$ — статистика критерия

-теста и размеры выборок совпадают, то

$t_j = \min_i\left\{T_{j,i}\right\} = \sqrt{n} \min_{ \neq j} \left\{\frac{\overline{X}_{\cdot, j} - \overline{X}_{\cdot, i}}{S_{j,i}} \right\}, \quad S_{j,i}^2 = S_j^2 + S_i^2.$

Можно доказать, что при нулевой гипотезе и неизвестных дисперсиях существует предельное распределение

$t_j = \sqrt{n} \min_{i \neq j}\left\{\frac{\overline{X}_{\cdot, j} - \mu_j}{S_j} \frac{1}{\sqrt{1 + \frac{S_i^2}{S_j^2}}} - \frac{\overline{X}_{\cdot, i} - \mu_i}{S_i} \frac{1}{\sqrt{1 + \frac{S_j^2}{S_i^2}}} \right\} \to \\ \to \min_{i \neq j} \left\{\frac{Z_j}{\sqrt{1 + \frac{\sigma_i^2}{\sigma_j^2}}} - \frac{Z_i}{\sqrt{1 + \frac{\sigma_j^2}{\sigma_i^2}}}\right\}, \quad n \to +\infty,$

где Z_i, Z_j независимы и имеют стандартное нормальное распределение. Стоит отметить, что величины под минимумом зависимы — везде присутствует Z_j . Но предельное распределение зависит только от дисперсий.

Критическое множество будет иметь вид

$\{t_j > c_j\}.» src=«https://habrastorage.org/getpro/habr/upload_files/1d4/03a/93a/1d403a93a846d6fc259e17ccbf75dd9a.svg» />Константу <img alt=$ для каждого

можно выбрать с помощью Монте-Карло для заданного $\alpha_j$ так, чтобы

$\mathbf{P}_{H_0}(t_j > c_j) = \alpha_j = \alpha / k.» src=«https://habrastorage.org/getpro/habr/upload_files/ff3/200/79e/ff320079e9352d1282f21006fff909e6.svg» />Будем считать, что при гипотезе <img alt=$ при различных

вероятность ошибки первого рода будет одна и та же.

Чтобы посчитать размер выборки нужно зафиксировать отклонение и вероятность ошибки второго рода $\beta$ . Рассмотрим $\widetilde{H}_j: \mu_j = d + \mu_1 = \ldots = d + \mu_k$ . Тогда

$\mathbf{P}_{\widetilde{H}_j}(t_j > c_j) = 1 — \beta,» src=«https://habrastorage.org/getpro/habr/upload_files/a1d/53d/958/a1d53d958e80d9f26a112d01a1a79180.svg» />где<img alt=$

Дальше можно моделировать для разных n_j желаемое $\beta$ и по виду кривой понять, какой n_j стоит выбрать для каждого . Положим:

$n = \max_j n_j.$

Отдельно рассмотрим случай равных дисперсий при нулевой гипотезе, поскольку нередко при проведении тестов при H_0 предполагаются равные дисперсии $\sigma_1^2 = \dotsc = \sigma_k^2 = \sigma^2$ . Получаем, что предельное распределение имеет вид

$t_j \xrightarrow{d} \frac{1}{\sqrt{2}} \min_i \left\{Z_1 - Z_i \, | \, i \neq 1\right\}, \quad n \to +\infty.$

где сходимость подразумевается по распределению. При нулевой гипотезе H_0 в пределе t_j имеют некоторое одинаковое распределение и нужно определить только одну константу для критического множества $\{t_j > c\}» src=«https://habrastorage.org/getpro/habr/upload_files/bce/78e/a3c/bce78ea3ca9e77808c287d1c70ce9093.svg» /> которая является <img alt=$ -квантилем распределения . Обозначим $c = c_{1-\alpha/k}$ .

Определять размер выборки будем аналогично. В силу того, что мы знаем распределение t_j при гипотезе H_0, верно равенство

$\mathbf{P}_{\widetilde{H}_j}(t_j > c_{1-\alpha/k}) = \mathbf{P}_{H_0}\left (t_j > c_{1-\alpha/k} — \sqrt{n} \frac{d}{\sqrt{2 \sigma^2}}\right) = 1 — \beta.» src=«https://habrastorage.org/getpro/habr/upload_files/15f/7c9/4ca/15f7c94ca1f48ca94ce731afbc7d967c.svg» />Следовательно, верно <img alt=$

где $c_\beta$ — $\beta$ -квантиль распределения . Таким образом, мы получаем явное выражение для

$n = \frac{2 \sigma^2 (c_{1-\alpha/k} - c_{\beta})^2}{d^2}.$

Что и требовалось доказать.

Мы пришли к тому, что при множественном тестировании выборок можно рассматривать пределы используемых в критерии статистик при достаточно большом размере одной выборки. Это возможно, поскольку для теста требуется много независимых экспериментов. Так, если некоторая -я выборка стат. значимо лучше каждой другой выборки, принимается гипотеза H_i, где $i = 1, \dotsc, k,$ иначе принимается гипотеза H_0 . Математически критерий теста описан в доказательстве.

Моделирование. Мы провели математический разбор критерия, основанного на предельном распределении, который будем называть оптимальным решением. И снова возникает вопрос: решает ли этот метод проблемы, возникшие при попарном сравнении выборок?

Промоделируем частоту неверного отклонения нулевой гипотезы для предыдущего примера для распределения Бернулли.

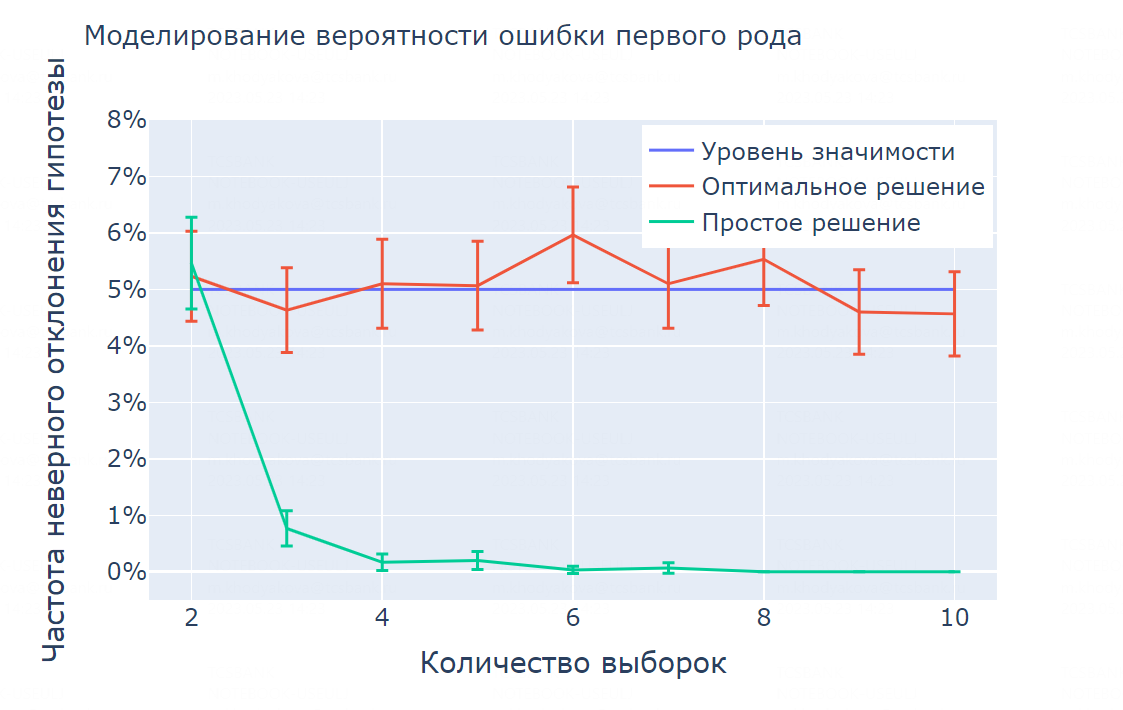
При увеличении количества выборок частота неверного отклонения нулевой гипотезы уже не убывает к нулю, а близка к уровню значимости 5%, который мы заложили.

Мы добились того, чего хотели. Посмотрим, как это влияет на минимальный размер одной выборки.

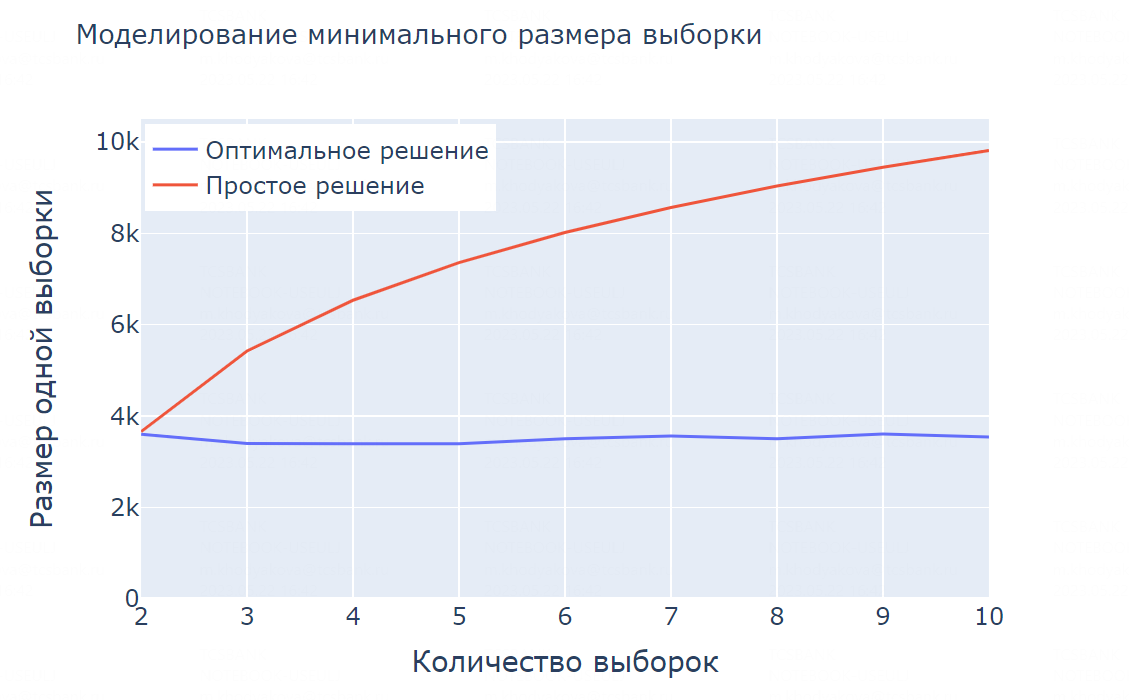
Размер выборки уже не растет при увеличении количества выборок, а остается примерно на одном уровне. Это положительно скажется на длительности теста.

Например, мы решили провести тест десяти выборок, выбрав конверсию целевой метрикой. Тогда при использовании оптимального решения тест займет в три раза меньше времени, чем при использовании простого решения.

Как пользоваться методом, основанным на предельном распределении

Чтобы каждый раз не писать код, мы с коллегами из Сбера оформили инструмент для использования метода, основанного на предельном распределении. Мы создали функции критерия, минимального размера выборки и квантиля предельного распределения в библиотеке HypEx для Python.

Пример кода:

import hypex.abn_test as criteria

alpha = 0.05                                                   # Уровень значимости
beta = 0.2                                                     # Вероятность ошибки II рода
sample_count = 10                                              # Количество выборок
d = 0.02                                                       # MDE

# Считаем минимальный размер выборки
n = criteria.min_sample_size(number_of_samples=sample_cont,
                             minimum_detectable_effect=d,
                             variances=hist_var,               # Оценка дисперсии по историческим данным
                             significance_level=alpha,
                             power_level=beta,
                             equal_variance=True)

# Номер принятой гипотезы
res = test_on_marginal_distribution(sample_list,               # Массив выборок
                                    significance_level=alpha)

Перейдя по ссылкам, можно посмотреть

Заключение

Мы построили метод множественного тестирования, который позволяет нам ошибаться ровно с той вероятностью, которую мы закладываем. А еще создали инструмент для реализации теста. Построенный метод дает нам возможность не увеличивать размер одной выборки и проводить множественное тестирование быстрее в несколько раз.

Надеюсь, эта статья будет вам полезна на практике. Если есть вопросы, оставляйте их в комментариях.